Transformer-Based Authorship Verification Research

Overview: In this research, I implemented Ibrahim et al.'s (2023) state-of-the-art Siamese SBERT architecture for historical document verification. I achieved near-perfect metrics across multiple distorted views while handling genre/topic bias through novel dataset construction and text distortion techniques from Stamatatos (2017).

Executive Summary Video

A comprehensive overview of the Siamese SBERT architecture implementation for authorship verification, including key findings from the analysis of the Pickett love letters.

Historical Context

This research tackles a longstanding historical question concerning love letters attributed to Confederate General George E. Pickett, published posthumously by his wife LaSalle Corbell Pickett. As a prolific author with no other verified works by the General available, the letters' authenticity has been debated by historians. This presents an ideal case for authorship verification (AV) - determining if two texts share the same author.

Architecture & Implementation

 flowchart TD
     subgraph "(B) SBERT Training"
         lilat["LILAtrain"] --> batch1
         batch1["
$$B = \{(c_{\text{a}}, c_{\text{o}})_i\}_{i=1}^{\text{batch\_size}}$$
"]  --> ca1["$$C_{\text{a},i}$$"]
         batch1 --> ca2["$$C_{\text{o},i}$$"]
         ca1 --> bert1[SBERT]
         ca2 --> bert2[SBERT]
         bert1 --> pool1[Mean Pooling]
         bert2 --> pool2[Mean Pooling]
         pool1 --> ea1["$$E_{\text{a},i}$$"]
         pool2 --> eo1["$$E_{\text{o},i}$$"]
         ea1 --> contrastive[Contrastive Loss]
         eo1 --> contrastive
     end

     subgraph "(A) SBERT at Inference"
         lilai["LILAinfer"] --> batch2
         batch2["
$$B = \{(c_{\text{a}}, c_{\text{o}})_i\}_{i=1}^{\text{batch\_size}}$$
"]  --> ca3["$$C_{\text{a},i}$$"]
         batch2 --> ca4["$$C_{\text{o},i}$$"]
         ca3 --> bert3[SBERT]
         ca4 --> bert4[SBERT]
         bert3 --> pool3[Mean Pooling]
         bert4 --> pool4[Mean Pooling]
         pool3 --> ea2["$$E_{\text{a},i}$$"]
         pool4 --> eo2["$$E_{\text{o},i}$$"]
         ea2 --> cos["Cosine Similarity"]
         eo2 --> cos
         cos --> rescale["Rescaling"]
         rescale --> sim["Similarity Score [0, 1]"]
     end
     style contrastive fill:#9999ff
     style contrastive color:#000000
     style cos fill:#ff9999
     style cos color:#000000
     style rescale fill:#ff9999
     style rescale color:#000000
     style sim fill:#ff9999
     style sim color:#000000
     style lilat fill:#999999
     style lilat color:#000000
     style lilai fill:#999999
     style lilai color:#000000
Figure 1: Model architecture showing (A) inference time configuration with cosine similarity output and (B) training time configuration with contrastive loss. Both utilize identical BERT encoders and mean pooling layers.
Key Technical Innovation: Discovered and resolved a contradiction in Ibrahim et al.'s architecture where the stated contrastive loss function was incompatible with their output layer configuration. Successfully implemented a modified architecture maintaining SOTA performance while ensuring theoretical soundness.

Modified Contrastive Loss Implementation

Building on Hadsell, Chopra, and LeCun's foundational work (2006), implemented a modified contrastive loss function that allows for more nuanced control over embedding space distances. The implementation uses separate margin parameters for same-author and different-author pairs, enabling finer control over the model's discriminative behavior.

For same-author pairs: \[y_{same} = y \cdot F_{relu}(\text{margin}_s - x)^2\] For different-author pairs: \[y_{diff} = (1-y) \cdot F_{relu}(x - \text{margin}_d)^2\] Final loss: \[L = 0.5(y_{same} + y_{diff})\] Where \(x\) is the cosine similarity scaled to [0,1], \(y\) is the ground truth (1 for same-author, 0 for different-author), \(F_{relu}\) is the rectified linear unit function, and \(\text{margin}_s\) and \(\text{margin}_d\) control the boundaries of the loss-accruing regions in the embedding space for same-author and different-author pairs respectively.
Implementation Note: While traditional modified contrastive loss implementations typically work with a similarity range of [-2, 0], I maintained a [0, 1] range through cosine similarity rescaling. This preserves the relative embedding distances crucial for contrastive learning while allowing for seamless integration with the broader architecture. This modification demonstrates the flexibility of contrastive learning approaches, as relative distances, not absolute scales, drive the learning dynamics. 
class ModifiedContrastiveLoss(nn.Module):
    def forward(self, anchor, other, labels):
        # Calculate cosine similarity and rescale to [0,1]
        similarities = (F.cosine_similarity(anchor, other) + 1) / 2

        # Modified loss with separate margins for same/different pairs
        same_author_loss = labels.float() * \
            F.relu(self.margin_s - similarities).pow(2)
        diff_author_loss = (1 - labels).float() * \
            F.relu(similarities - self.margin_d).pow(2)

        # Balance contribution of positive and negative pairs
        losses = 0.5 * (same_author_loss + diff_author_loss)
        return losses.mean()
Enhancement: This modified implementation allows for flexible tuning of both the "push" and "pull" forces in the embedding space, leading to more stable training and better generalization.

Dataset Construction & Preprocessing

Developed LILA (Love letters, Imposters, LaSalle Augmented), a carefully balanced dataset with: 

flowchart LR
    subgraph Disk["On-Disk Preprocessing"]
        style Disk fill:#e6f3ff,stroke:#333

        %% A -> B (subgraph) -> C
        A[("Raw Text Files")] --> B

        %% Turn B into a subgraph named "Text Normalization"
        subgraph B["Text Normalization"]
            D[Lowercase] --> E[Collapse Whitespace] --> F[Strip Special Characters]
        end

        B --> C{"Distorted View Generation"}

        C --> |"$$k_{view} = len(W_{LILA})$$"|G1[("Undistorted View")]
        C --> |"$$k_{view} = 20000$$"|G2[("Lightly Distorted")]
        C --> |"$$k_{view} = 3000$$"|G3[("Moderately Distorted")]
        C --> |"$$k_{view} = 300$$"|G4[("Heavily Distorted")]
    end

    subgraph LILA["LILADataset"]
        style LILA fill:#ffe6e6,stroke:#333
        G1 & G2 & G3 & G4 --> H[["Tokenization"]]
        H --> I[["Fixed-Length Chunking"]]
        I --> t["Generate K-Fold Train/Val Pairs"]
        I --> i["Generate Inference Pairs"]
    end

    classDef storage fill:#ff9,stroke:#333
    classDef process fill:#fff,stroke:#333
    classDef decision fill:#9cf,stroke:#333

    class A,G1,G2,G3,G4 storage
    class B,D,E,F process
    class C decision
Figure 2: LILA data processing pipeline showing on-disk preprocessing and LILADataset construction.

Text Distortion Implementation

def dv_ma(text, W_k):
    """
    Replace words not in W_k (k most frequent words) with
    asterisk strings of equal length.
    """
    words = text.split()
    for i, word in enumerate(words):
        if (word.lower() in W_k):
            continue
        else:
            words[i] = re.sub(r'[^\d]', '*', word)
            words[i] = re.sub(r'[\d]', '#', words[i])
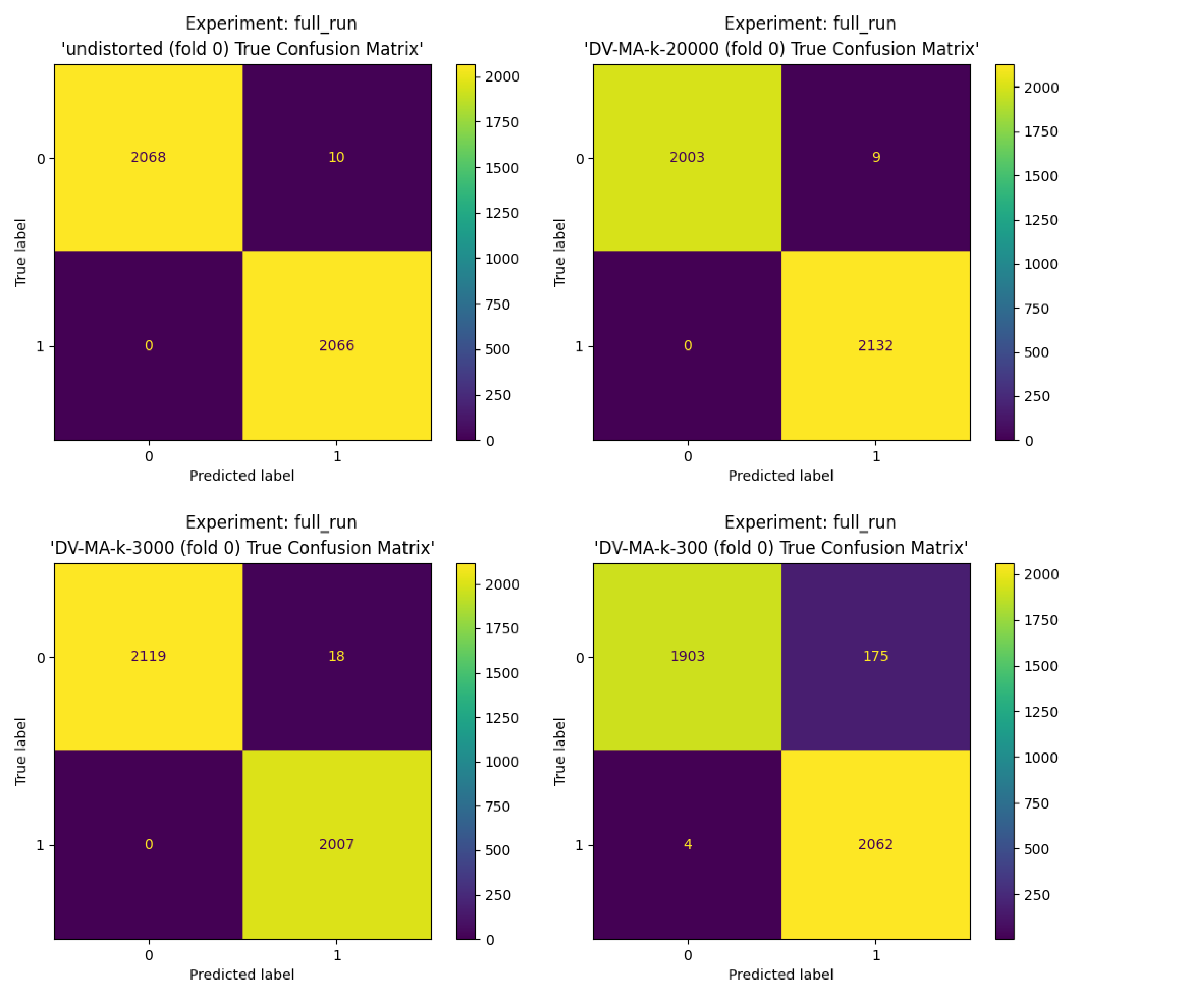
    return ' '.join(words)

Results & Analysis

Figure 3: Loss plots for all five folds across four views, showing clear convergent behavior with stability increasing as distortion level increases.
View AUC C@1 F1 F0.5u
Undistorted 1.000 ± 0.000 0.998 ± 0.003 0.998 ± 0.003 0.996 ± 0.005
k=20,000 1.000 ± 0.000 0.996 ± 0.007 0.996 ± 0.006 0.992 ± 0.012
k=3,000 1.000 ± 0.000 0.994 ± 0.003 0.994 ± 0.003 0.990 ± 0.006
k=300 0.991 ± 0.001 0.964 ± 0.008 0.966 ± 0.007 0.943 ± 0.010

External Validation on VALLA Dataset

To validate the model's generalizability, I evaluated performance on the PAN20 sub-split of the VALLA benchmark, a comprehensive AV benchmark introduced by Tyo et al. (2022). My implementation achieved competitive results against PAN 2020 shared task participants:

Model Overall Score Training Data
PAN20 Winner (Boenninghoff et al.) 0.897 PAN20-small
Our Implementation (30 epochs) 0.801 VALLA (more challenging)
PAN20 Baseline 0.747 PAN20-large
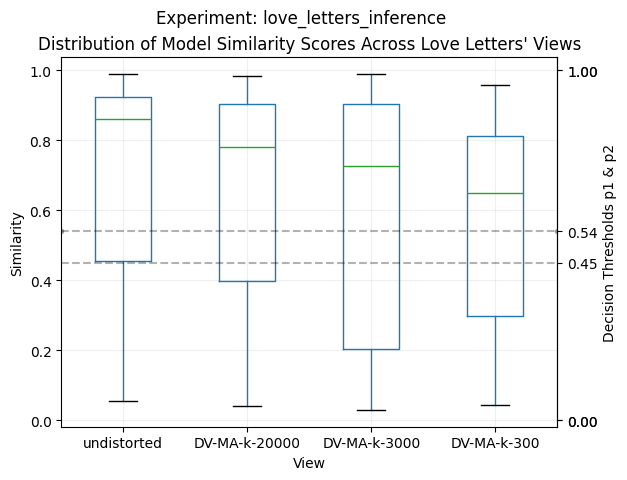
Note: Despite using VALLA's more challenging formulation which removes genre/topic/class-balance bias, my implementation achieved the equivalent of a 5th place team in PAN 2020 models using the same raw data, demonstrating strong generalization capability.

Inference Results on the Love Letters

The model's analysis of the letters shows a consistent and strong pattern of attribution to LaSalle's authorship across all distortion views:

Distorted View Mean Similarity Same-Author Different-Author Undecided
Undistorted 0.709 ± 0.298 74.4% 24.8% 0.9%
k=20,000 0.661 ± 0.296 68.2% 27.6% 4.2%
k=3,000 0.598 ± 0.334 60.1% 34.7% 5.1%
k=300 0.564 ± 0.272 57.8% 37.5% 4.7%
Figure 4: Distribution of similarity scores across different distortion views for the love letters. Decision thresholds p1 and p2 shown as dashed lines.
Key Finding: The model demonstrates strong attribution to LaSalle's authorship, with 74.4% same-author predictions in the undistorted view. This signal persists even under heavy distortion (k=300), where topic and content-specific features are largely masked, indicating deep stylistic similarities between the letters and LaSalle's known works. Notably, the highest-similarity passages contain anachronistic references independently identified by historians as problematic, providing computational support for historical observations about the letters' authenticity.

Technical Infrastructure

Figure 5: Confusion matrices across distortion views showing consistent discriminative ability even with heavy distortion (k=300).